箱ひげ図の見方・書き方を解説！一瞬で伝わるレポート資料の作り方

株式会社ロックオン、マーケティングメトリックス研究所の松本です。

これまでにもferretにて、"誰が見ても一瞬で伝わるレポート資料の作り方"をテーマにした折れ線グラフや散布図、ヒストグラム、円グラフについて説明しました。

直感的にデータを把握することができるグラフを活用することで、資料は見違えるように良質に生まれ変わります。今回はあまり聞きなれないものかもしれませんが、ヒストグラム同様にデータのばらつき具合を示すのに用いられる「箱ひげ図」の使い方を紹介します。

参考：
誰が見ても一瞬で伝わるレポート資料の作り方｜ferret
誰が見ても一瞬で伝わるレポート資料の作り方折れ線グラフの使い方をマスターする編｜ferret
円グラフの使い方をマスターしよう〜誰が見ても一瞬で伝わるレポート資料の作り方｜ferret
ヒストグラムを使って誰が見ても一瞬で伝わるレポート資料を作る方法｜ferret
　　

箱ひげ図とは何を最も伝えたい時に使うのか

箱ひげ図は、ヒストグラムと同じくデータの"散らばり"を表すのに用います。データが満遍なく散らばっているのか、一定範囲に集中しているのか、その偏り具合を表現するのに適しています。

箱ひげ図と言われても、聞き馴染みがないかもしれません。もしかしたら「株価を表すグラフのことですか？」と思い浮かべる方もおられるでしょう。あれはローソク足といって、姿形は似ていますが厳密に言えば違います。

箱ひげ図は、2012年に改訂された新学習指導要領に基づいて、高校数学Ⅰにも登場するようになりました。このコンテンツを読まれている皆さんは習ったことがないかもしれませんが、いずれ社会人として皆さんの勤める会社に入社する新入社員は知っているグラフです。

このコンテンツをキッカケに知って貰えれば幸いです。
　　

箱ひげ図の見方について

箱ひげ図は、長方形の箱と、箱からニョキッと伸びる棒（これが”ひげ”です）で構成されています。それぞれに意味と役割を持っています。

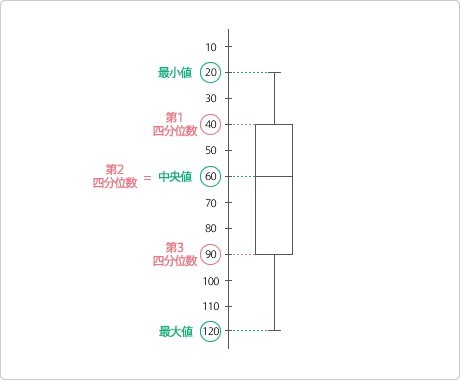
長方形の箱の真ん中の線は「中央値」です。データを小さい順（大きい順）に並べた時に、個数で見て真ん中に位置する値を中央値といいます。これが、データの集まりの「中心」を表しています。

箱の両端である「第1四分位」と「第3四分位」は、データを小さい順（大きい順）に並べた時に、個数で見てちょうど4分の1（3）に位置する値を第1（3）四分位といいます。25%目、75％目が「第1四分位」と「第3四分位」なのです。この理屈で、中央値は第2四分位（50%）ともいえます。

最後の「ひげ」の部分、これはデータを小さい順（大きい順）に並べた時に、一番小さい（大きい）データを表しています。「ひげ」の部分からデータが始まり、「ひげ」の部分でデータが終わります。つまり、箱ひげ図とは、データを順番に並べて、始まり、全体の4分の1、4分の2、4分の3、終わりに達した地点にマークをしているだけのグラフなのです。

そして、データの真ん中を表す中央値（4分の2）を中心に、上下にどれくらい「散らばっている」か確認することができます。第1四分位と第3四分位の間（25%〜75%の間）を「四分位範囲」と呼び、この範囲が狭ければ真ん中にデータが集まっていますし、範囲が広ければデータが散らばっていると言えます。

箱ひげ図は、まず中央値と四分位範囲を見ることから始まると言ってもいいでしょう。

ちなみに、箱ひげ図はoffice2016から作成できるようになりました。これまでは直ぐに作れないので世間になかなか浸透しませんでしたが、いよいよ誰もが直ぐに簡単に作れるようになります。
　　

なぜデータの真ん中を表すのに「平均」は使わないのか

データの真ん中を表すなら「平均」でも良いのではないか、と皆さんは思われるかもしれません。それは全く違います。

以下のあるグループのデータを見てください。9人それぞれの年収を記載しています。この9人の「真ん中」は年収何万でしょうか。

平均を求めると合計5,100万÷9人で約567万になります。一方、中央値を求めると5人目の年収ですから400万になります。

どちらの計算式も間違っていません。データの真ん中を表現するのに適した表現方法はどちらか？という話です。

データの中にほかと比べて極めて大きいデータが含まれていた場合、そのデータまで考慮して「真ん中」を求めてしまうのが平均です。一方で、データ全体を考慮せずに並び順で見て「真ん中」を見るのが中央値です。実際、平均約567万という値は、年収2,000万以外の8人の年収を上回っています。

ただ、中央値もデータを意図的に造ることがあります。それはデータの個数が偶数だった場合です。真ん中を求める場合、個数が奇数であればその値を使えますが、偶数であれば真ん中が2つのデータになります。

先ほどのグループから年収2,000万が脱退すると、以下のような8人で構成されます。
この8人の「真ん中」は年収何万でしょうか。

この場合、4人目と5人目の2人分の平均が「真ん中」になります。約388万が中央値ということになります。
隣り合う2つのデータの平均であれば、先ほどのような大きなズレは生じないだろうという発想です。
　　

こんなにも伝わりやすい！箱ひげ図の見せ方

箱ひげ図は、複数並べて比較できるというメリットがあります。

以下のグラフは2006～2015年の10年間のプロ野球パ・リーグの順位毎の勝率を箱ひげ図で表しています。図からは、どんなにダメなチームでも勝率が4割ほどあるし、どんなに強いチームでも勝率は7割を下回ることがわかります。

次に、各順位の「箱」が、隣り合う順位の箱と若干重なり合っていることもわかります。

例えば、1位と2位を見てみると、2位の第3四分位は、1位の第1四分位を上回っています。つまり、10年という括りで見たら1位より2位のチームが強いという可能性もあるわけです。野球とは、絶対的な強さではなく、あくまで他球団と比べた相対的な強さを競い合うゲームであることがわかります。

また、2位や3位に比べて1位の四分位範囲が広いことがわかります。これは他チームを押しのけてブッチギリの優勝を決めた年と、2位とデッドヒートを繰り広げながら何とか優勝を決めた年の2種類があるということです。

最近のプロ野球はポストシーズン制度が導入され、何とか3位までに滑り込めれば日本シリーズに出場できる可能性が与えられます。つまり、4位を上回る成績を収めれば良いわけです。4位の最大値は勝率0.524ですから、ここ10年という縛りはあるものの、その勝率を越えればまず出場は間違いないと考えて良いでしょう。

箱ひげ図を見るだけで、こんなことが瞬時にわかるのです。
　　

異常に高い値が含まれていた場合の書き方

先ほどの9人組のグループのデータは1人だけ年収2,000万と突出した値が含まれていました。こうした他と比べて大きく外れた値を「異常値」または「外れ値」と言います。

箱ひげ図では、「異常値」をどのように表示するのが適切なのでしょうか。「第3四分位」である450万から2,000万まで長い「ひげ」を書くべきでしょうか。

私たちは、この箱ひげ図が表すデータの内訳を知っていますが、初見の人はデータの第３四分位から最大値までどんなデータが含まれているのか考えてしまうでしょう。箱ひげ図のマナーとして、こうした「異常値」はとしてひげに含めません。点をうって、その1つ前の値まで線を引きます。9人組のデータであれば、2,000万の前の475万まで線を引きます。

"異常値"と見なす基準は、四分位範囲の値の1.5倍を第1四分位と第3四分位から数えて上回るか否かと決まっています。

今回のデータの場合、四分位範囲は100万です。したがって「150万」が基準です。第1四分位である年収350万から150万を引いた200万を下回る値は外れ値ですし、第3四分位である年収450万から150万を足した600万を上回る値は外れ値です。よって年収2,000万は外れ値とみなされます。外れ値を考慮した上で箱ひげ図を読むと、よりデータの散らばりを理解できます。

以下の図は、イタリアと日本の首相たちの在任期間を箱ひげ図で表しています。

　　

箱ひげ図からは様々な推測が立てられる

イタリアの外れ値はベルルスコーニで在任期間は3,339日。日本の外れ値はそれぞれ佐藤栄作2,798日、吉田茂2,616日、小泉純一郎1,980日、中曽根康弘1,806日です。

日本で言えば、この4人は「外れ値」と見なせるほど長期政権を築いた稀有な存在であると言えます。イタリアの四分位範囲は日本より長い分、ひげも日本より長いですね。ただし中央値で見ると、日本よりイタリアのほうが短いことがわかります。すなわち長く続かなかった政権と、長期に築いた政権の2パターンに別れることがわかります。

散布図は、見れば見るほど「この結果はどういうことだろう？」「この違いは何が理由だろう？」と考えさせられます。

中央値や四分位範囲など、かなり初歩的な統計データしか使っていません。したがって1度勉強すれば誰もが簡単に理解し使いこなせるグラフだと言えます。